数据结构和算法之美-第七篇-递归

前言

说起算法，提的最多的就是递归、排序和二分查找，因为这些是最基础也是最经常使用的。实际工作中，递归也是一种很有效的算法或者说编程技巧。

不过有些时候总觉得递归没那么好写，得琢磨半天。。。

如何理解递归

或者说什么样的问题可以用递归来解决。

一个问题的解可以被拆成几个子问题的解
这个问题与分解而出的子问题，除了数据规模不同，求解思路完全一致
存在递归终止条件，一般就是数据规模到达可以预知的最小就是终止条件。

符合这种要求的问题就可以使用递归解决。比如经典的斐波那契数列：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…… 第 n 号位置数值是第 n-1 号位置的数和第 n-2 号位置的数的和。比如现在问题就是求第 10 号位置的数，这个问题就可以被拆成求第 9 号位置的数和第 8 号位置的数；相比原问题，n 的值变小了，但求第 9 号位置的数和第 8 号位置的数和原问题的思路一致；直到（终止条件）第 0 号位置的值为 0，第 1 号位置的值为 1

如何编写递归代码

写递归代码的关键是写出递归公式，找出终止条件。

举个栗子：
假如这里有 n 个台阶，每次你可以跨 1 个台阶或者 2 个台阶，请问走这 n 个台阶有多少种走法？如果有 7 个台阶，你可以 2，2，2，1 这样子上去，也可以 1，2，1，1，2 这样子上去，总之走法有很多，那如何用编程求得总共有多少种走法呢？
我们仔细想下，实际上，可以根据第一步的走法把所有走法分为两类，第一类是第一步走了 1 个台阶，另一类是第一步走了 2 个台阶。所以 n 个台阶的走法就等于先走 1 阶后，n-1 个台阶的走法加上先走 2 阶后，n-2 个台阶的走法。用公式表示就是：
f(n) = f(n-1)+f(n-2)
有了递推公式，递归代码基本上就完成了一半。我们再来看下终止条件。当有一个台阶时，我们不需要再继续递归，就只有一种走法。所以 f(1)=1。这个递归终止条件足够吗？我们可以用 n=2，n=3 这样比较小的数试验一下。
n=2 时，f(2)=f(1)+f(0)。如果递归终止条件只有一个 f(1)=1，那 f(2) 就无法求解了。所以除了 f(1)=1 这一个递归终止条件外，还要有 f(0)=1，表示走 0 个台阶有一种走法，不过这样子看起来就不符合正常的逻辑思维了。所以，我们可以把 f(2)=2 作为一种终止条件，表示走 2 个台阶，有两种走法，一步走完或者分两步来走。
所以，递归终止条件就是 f(1)=1，f(2)=2。这个时候，你可以再拿 n=3，n=4 来验证一下，这个终止条件是否足够并且正确。
我们把递归终止条件和刚刚得到的递推公式放到一起就是这样的：

1
2
3

f(1) = 1
f(2) = 2
f(n) = f(n - 1) + f(n - 2)

转换成代码也就是：

function foo(n){
  if(n === 1) return 1
  if(n === 2) return 2
  return foo(n - 1) + foo(n - 2)
}

为何递归难以理解

人脑几乎没办法把整个“递”和“归”的过程一步一步都想清楚。计算机擅长做重复的事情，所以递归正和它的胃口。而我们人脑更喜欢平铺直叙的思维方式。当我们看到递归时，我们总想把递归平铺展开，脑子里就会循环，一层一层往下调，然后再一层一层返回，试图想搞清楚计算机每一步都是怎么执行的，这样就很容易被绕进去。
对于递归代码，这种试图想清楚整个递和归过程的做法，实际上是进入了一个思维误区。很多时候，我们理解起来比较吃力，主要原因就是自己给自己制造了这种理解障碍。那正确的思维方式应该是怎样的呢？

如果一个问题 A 可以分解为若干子问题 B、C、D，你可以假设子问题 B、C、D 已经解决，在此基础上思考如何解决问题 A。而且，你只需要思考问题 A 与子问题 B、C、D 两层之间的关系即可，不需要一层一层往下思考子问题与子子问题，子子问题与子子子问题之间的关系。屏蔽掉递归细节，这样子理解起来就简单多了。

因此，编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤

递归需要两个问题

堆栈溢出

函数调用会使用栈来保存临时变量。每调用一个函数，都会将临时变量封装为栈帧压入内存栈，等函数执行完成返回时，才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

JavaScript的还是调用同样是以栈的方式维护，详情可以参考JS进阶系列-第四篇-执行上下文
函数调用栈是有层级限制的，不同的浏览器的限制可能不相同。

重复计算

递归的代码很容易出现重复计算的问题，比如上面那个楼梯走法的问题，如果我们把整个递归过程分解一下，就是这样的：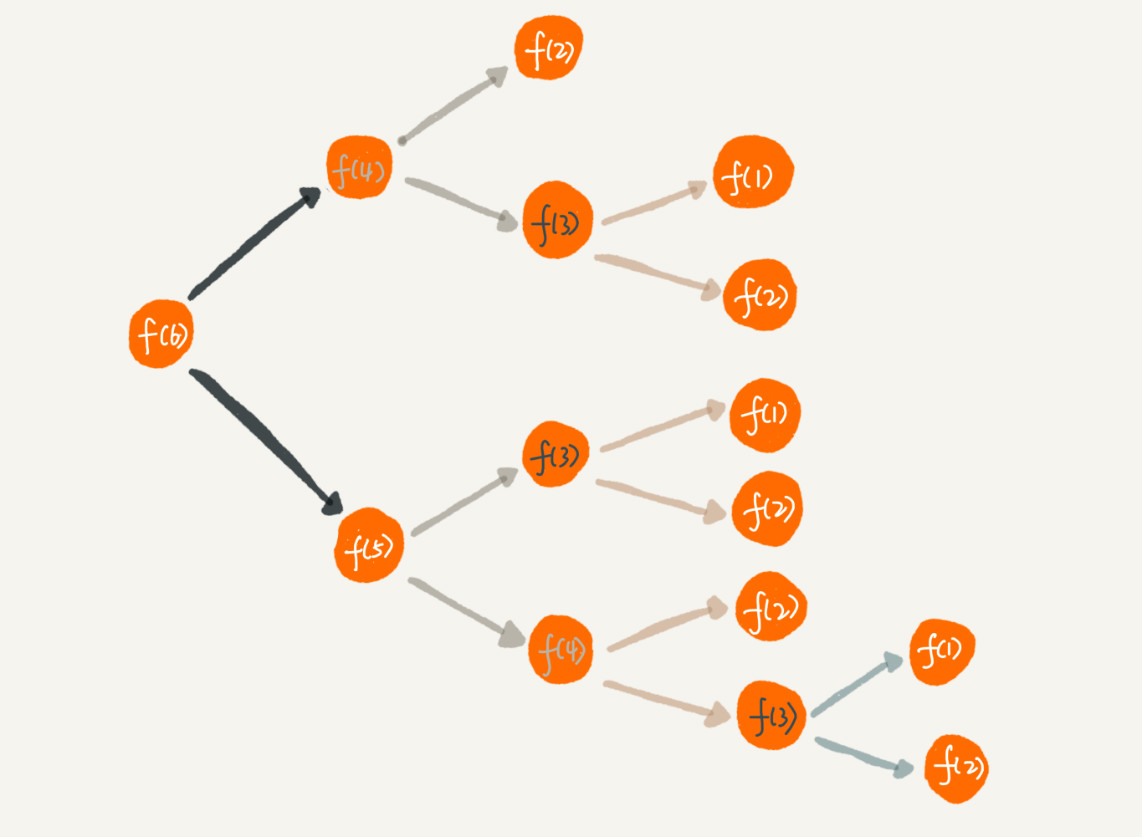
data-structures-algorithm 2019-07-31 下午4.13.13.jpg

想要计算 f(6) 需要先计算 f(5) 和 f(4) ，计算 f(5) 需要先计算 f(4) 和 f(3) ，f(4) 被重复计算。从图中可以看出 f(3) 也出现了很多重复计算。

为了避免重复计算，我们可以通过一个数据结构（比如散列表）来保存已经求解过的 f(k)。当递归调用到 f(k) 时，先看下是否已经求解过了。如果是，则直接从散列表中取值返回，不需要重复计算，这样就能避免刚讲的问题了。
稍微改造一下代码

const tempF = {}
function foo(n){
  if(n === 1) return 1
  if(n === 2) return 2
  if(tempF.hasOwnProperty(String(n))) return tempF[String(n)]
  const ret = foo(n - 1) + foo(n - 2)
  tempF[String(n)] = ret
  return ret
}

递归和循环

递归有利有弊，利是递归代码的表达力很强，写起来非常简洁；而弊就是空间复杂度高、有堆栈溢出的风险、存在重复计算、过多的函数调用会耗时较多等问题。所以，在开发过程中，我们要根据实际情况来选择是否需要用递归的方式来实现。

还是那个楼梯走法的问题，用循环的方式为：

function foo(p){
  let m = 1; 
  let n = 2;
  let ret = 0;
  if(p === 1) return m
  if(p === 2) return n
  
  for(let i = 3 ; i <= p; i++){
    ret = m + n
    m = n
    n = ret
  }
  return ret 
}

那是不是所有的递归代码都可以改为这种迭代循环的非递归写法呢？

笼统地讲，是的。因为递归本身就是借助栈来实现的，只不过我们使用的栈是系统或者虚拟机本身提供的，我们没有感知罢了。如果我们自己在内存堆上实现栈，手动模拟入栈、出栈过程，这样任何递归代码都可以改写成看上去不是递归代码的样子。
但是这种思路实际上是将递归改为了“手动”递归，本质并没有变，而且也并没有解决前面讲到的某些问题，徒增了实现的复杂度。

前言