数据结构和算法之美-第九篇-归并排序、快速排序

归并排序

归并排序使用的是分治的思想，分治算法一般都是由递归实现的。回想一下递归的细节其实和分治很像，递归的思想一般是把一个大问题拆分成几个子问题，除了数据规模不同，子问题的求解思路和大问题没有任何区别。这种把大问题拆分成小问题的的思想其实就是一种分治的思想。而分治和递归的区别也在于此，分治是一种解决问题的思想，而递归是一种编程技巧。

归并排序
算法步骤：

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4. 重复步骤 3 直到某一指针到达序列尾
5. 将另一序列剩下的所有元素直接复制到合并序列尾

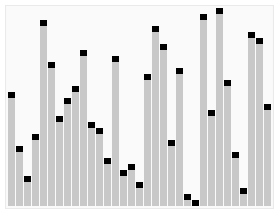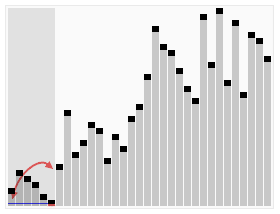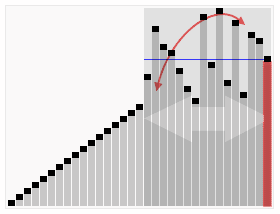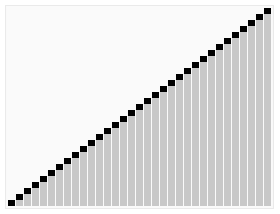
或者直接看 gif 图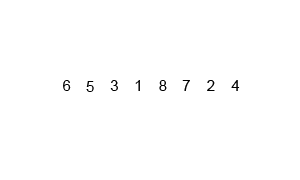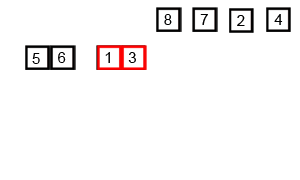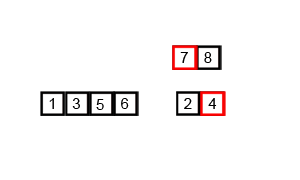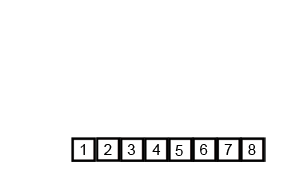

我们用递归来实现，难点在于如何找出它的递归公式以及终止条件。
拿到数组之后我们知道数组的起点和终点的下标，假设为 p 和 q，每次取中间点 r。那么公式也就是mergeArr(mergeSort(arr, p, r), mergeSort(r+1, q))，其中 mergeArr 是合并两个有序数组的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

const mergeArr = (arrL, arrR) => {
  let i = 0;
  let j = 0;
  const lenL = arrL.length;
  const lenR = arrR.length;
  const arr = [];
  while (i < lenL && j < lenR) {
    if (arrL[i] < arrR[j]) {
      arr.push(arrL[i]);
      i++;
    } else {
      arr.push(arrR[j]);
      j++;
    }
  }
  if (i === lenL) {
    arr.push(...arrR.slice(j, lenR));
  } else {
    arr.push(...arrL.slice(i, lenL));
  }
  return arr;
};
const mergeSort = (arr = [], p = 0, q) => {
  if (q === undefined) q = arr.length - 1;
  if (p >= q) return [arr[p]];
  const r = Math.floor((q + p) / 2);
  return mergeArr(mergeSort(arr, p, r), mergeSort(arr, r + 1, q));
};

归并排序是稳定排序
需要借助一个数组存储合并后的数组，空间复杂度是 O(n)，所以归并排序不是原地排序
归并排序使用的是递归，最好、最坏、平均情况时间复杂度都是 O(nlogn)

快速排序

快速排序同样是使用分治的思想。

快速排序

步骤为：

1. 挑选基准值：从数列中挑出一个元素，称为“基准”（pivot），
2. 分割：重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（与基准值相等的数可以到任何一边）。在这个分割结束之后，对基准值的排序就已经完成，
3. 递归排序子序列：递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。

和归并排序一样都是使用递归实现，我们可以直接以最后一个数做为基准数，比这个数大的我们放一个数组，比这个数小的我们放另一个数组，这样大问题就变成小问题了，然后小问题再继续拆分直到不能拆为止。但是这样空间复杂度是 O(n)，比起归并排序没有任何优势。快速排序其实可以是原地排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

const quickSort = (arr, p = 0, q) => {
  if (q === undefined) q = arr.length - 1;
  if (p < 0 || q < 0 || p >= q) return;
  const pointIndex = partition(arr, p, q);
  if (!pointIndex) return;
  quickSort(arr, p, pointIndex - 1);
  quickSort(arr, pointIndex + 1, q);
};

const partition = (arr, p, q) => {
  const point = arr[q];
  let j;
  for (let i = p; i < q; i++) {
    if (arr[i] < point) {
      if (j !== undefined) {
        const temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
        j++;
      }
    } else if (j === undefined) {
      j = i;
    }
  }
  if (j !== undefined) {
    const temp = arr[j];
    arr[j] = arr[q];
    arr[q] = temp;
  }
  return j;
};

通过partition实现原地排序，代价就是不稳定，相同大小的元素前后位置有可能发生变化。

快速排序的最好情况时间复杂度是 O(nlogn)，每次分区都及其均衡一分为二，最坏情况每次分区都极不均匀，时间复杂度退化成 O(n²)。平均时间复杂度是 O(nlogn)

总结

归并排序和快速排序使用的都是分治的思想，代码也都是通过递归来实现。找到递归公式是关键，代码的难点分别在于归并排序的 merge 函数以及快速排序的 partition 分区函数，其中 partition 分区函数非常巧妙，他是的快速成为了原地排序不过同时也变成了不稳定函数。

归并排序很稳定，时间复杂度永远都是 O(nlogn)。致命的缺点是空间复杂度是 O(n)。在数据规模比较大的情况因为此基本不会选择归并排序。

快速排序时间复杂度在极端情况下会退化成 O(n²)，不过几率很小，而且通过一些手段可以避免基准点选的这么差。这也是在实际开发中，使用快排的几率远大于归并的原因。

• ← Previous Post
• Next Post →