数据结构和算法之美-第二篇-浅析最好、最坏、平均、均摊时间复杂度

前言

我们已经知道如何分析一段代码的时间复杂度，这可以帮助我们写出更优秀的代码，在大多数情况下已经足够了。但在某些场景下，我们可能需要分析的再细致一些。比如具体某个性能调优的场景，我们知道数据规模的波动范围就能选择性的调整我们的代码。

最好、最坏情况时间复杂度

顾名思义。
最好情况时间复杂度：在最理想的情况下，执行这段代码的时间复杂度。
最坏情况时间复杂度：在最糟糕的情况下，执行这段代码的时间复杂度。
举个栗子：

1
2
3
4
5
6
7

function (arr =[], v){
  const n = arr.length
  for(let i = 0; i < n; i++){
    if(arr[i] === v) return i
  }
  return -1
}

这是查找数组中时候有指定值的一个例子，有就返回对应值的下标，否则返回-1
正常的分析，时间复杂度就是O(n)。
在这个例子中，最好的情况是数组的第一个值就是我们要找的值，时间复杂度就是O(1)，最糟糕的情况的是遍历完数组都没有找到，时间复杂度就是O(n)。

平均情况时间复杂度

我们都知道，最好情况时间复杂度和最坏情况时间复杂度对应的都是极端情况下的代码复杂度，发生的概率其实并不大。为了更好地表示平均情况下的复杂度，我们需要引入另一个概念：平均情况时间复杂度，后面我简称为平均时间复杂度。

还是上面那个例子
我们知道，要查找的变量 v，要么在数组里，要么就不在数组里。这两种情况对应的概率统计起来很麻烦，为了方便你理解，我们假设在数组中与不在数组中的概率都为 1/2。另外，要查找的数据出现在 0～n-1 这 n 个位置的概率也是一样的，为 1/n。所以，根据概率乘法法则，要查找的数据出现在 0～n-1 中任意位置的概率就是 1/(2n)。

回顾下高中数学期望的概念：

在概率论和统计学中，一个离散型随机变量的期望值是实验中每次可能出现的结果乘以其概率的总和。换句话说，期望值像是随机试验在同样的机会下重复多次，所有那些可能状态平均的结果，便基本上等同“期望值”所期望的数。

平均时间复杂度其实也就是求期望值，所以也叫期望时间复杂度，计算过程是：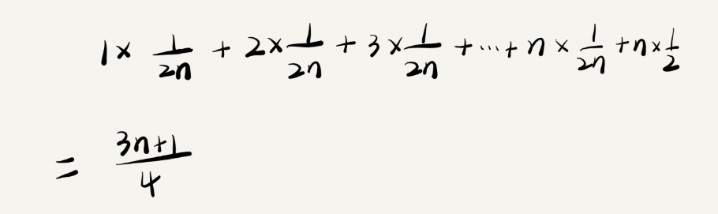

这样一看，时间复杂度的分析也太费劲了，这里再强调一下，多数情况我们不需要分析的这么细，只有在同一块代码，在不同的数据规模下，复杂度有量级的差距，这时候就需要好好分析一波了。

均摊时间复杂度

这个和平均情况时间复杂度有什么区别呢？

平均情况时间复杂度对应的情况通常是离散型随机变量，比如上面那个例子，指定值在不在数组中，每一次的可能性都是独立的。均摊时间复杂度则不同，它的整体是周期性的运行，通常是多个不耗时连续操作最后接一个耗时的操作，或者多个耗时的操作接一个不耗时的操作，不断周期连续运行。只要知道当前的时间复杂度，下一次的时间复杂度就可以预估，而平均情况时间复杂度只能整体用概率学的知识去统计。

举个均摊时间复杂度的例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14

let arr = []
function foo(v, n){
  const len = arr.length
  if(len >= n){
    let s = 0; 
    for(let i = 0; i < len; i++){
      s += arr[i]
    }
    arr = []
    return s
  }
  arr.push(v)
  return
}

如果数组的长度超过n，则返回数组中所有值的和，数组清空；否则把传入的值添加入数组，返回undefined。
这就是一个均摊情况的时间复杂的场景。在多数情况下，数组的长度不超过n，可以直接添加到数组，时间复杂度是 O(1)，等到数组长度为 n时，再次执行函数，需要进行遍历累加时间复杂度就是 O(n)，然后数组清空。后面继续前面的循环。
也就是说这个例子的时间复杂度是 O(1) O(1) O(1) … O(n) O(1) O(1) O(1)… O(n) O(1) …如此循环下去。把耗时多的那次操作均摊到接下来的 n-1 次耗时少的操作上，均摊下来，这一组连续的操作的均摊时间复杂度就是 O(1)。这就是均摊分析的大致思路。

和平均情况的时间复杂度例子对比，我们可以发现，均摊的例子中多数情况的时间复杂度是 O(1)，而平均的例子中只有很极端的情况下时间复杂度才是 O(1)。

其实均摊时间复杂度的场景范围要更小，通过这个例子以后我们遇到类似的场景通用样的手段相信很快就能分析出来。

• ← Previous Post
• Next Post →